Retrouver les cités perdues de l’âge du bronze grâce à la science économique

Plus on remonte dans le temps, plus les archéologues ont des difficultés à obtenir des informations fiables. La raison à cela est simple : petit à petit, le temps a raison des vestiges. Mais des méthodes nouvelles émergent pour pallier ce problème. Parmi elles : le recours à… la science économique !

[no_toc]

Dans un working paper sorti en novembre 2017, quatre économistes proposent d’aider à retrouver les cités perdues de l’âge du bronze grâce… à la science économique ! Leur stratégie consiste à exploiter une base de données de transactions commerciales pour identifier la position géographique probable d’un certain nombre de villes situées sur le territoire de l’actuelle Turquie.

Leurs résultats parfois confirment, parfois infirment, un certain nombre de théories pré-existantes. Et dans tous les cas, la démarche est fascinante.

Le premier tour de force de l’article de [zotpressInText item= »{MFK6S6PW} »] consiste en sa base de données : il s’agit d’une version numérisée de tablettes de marchands assyriens datant d’une période comprise entre -2000 et -1600 avant Jésus-Christ. Ces tablettes contiennent des informations comme les expéditions, les dépenses ou encore les contrats conclus avec d’autres marchands. Lorsqu’une tablette mentionne au moins deux villes, il est alors possible de dire que le marchand de la ville i a fait affaire avec un marchand de la ville j.

À partir de cette base de données, on reconstruit l’intensité des flux commerciaux entre les deux villes – plus exactement, le nombre de transactions qui ont lieu entre les deux villes :

\text{nb de transactions entre } i \text{ et } j = \text{nb de mentions de voyages entre } i \text{ et } j

Pour ensuite savoir où se situent les villes, les chercheurs utilisent un modèle bien connu en commerce international : le modèle gravitaire. Comme son nom le suggère, il s’agit d’une adaptation au commerce du modèle de gravité de Newton.

En règle général, on utilise ce modèle de la façon suivante : à partir de la taille de deux pays, villes, etc., on prédit une intensité du flux commercial. Et on compare cette prédiction aux données pour vérifier la validité du modèle.

Ici, les chercheurs procèdent à l’inverse : à partir de l’intensité des flux commerciaux reportée dans leur base de données, ils vont estimer les tailles et distances probables des villes. Et avec un jeu de contraintes trop compliqué à expliquer simplement, ils établissent une distribution géographique – en d’autres termes, une carte.

Pour s’assurer que leur démarche soit robuste, ils testent leur stratégie avec des villes dont la localisation géographique est connue : en estimant cette localisation à partir de la base de données, de combien le modèle se trompe par rapport à la vraie localisation ? Ils arrivent ainsi à retrouver à quelques dizaines de kilomètres près les villes principales (ce qui est un bon résultat), mais le modèle est moins précis pour les villes secondaires.

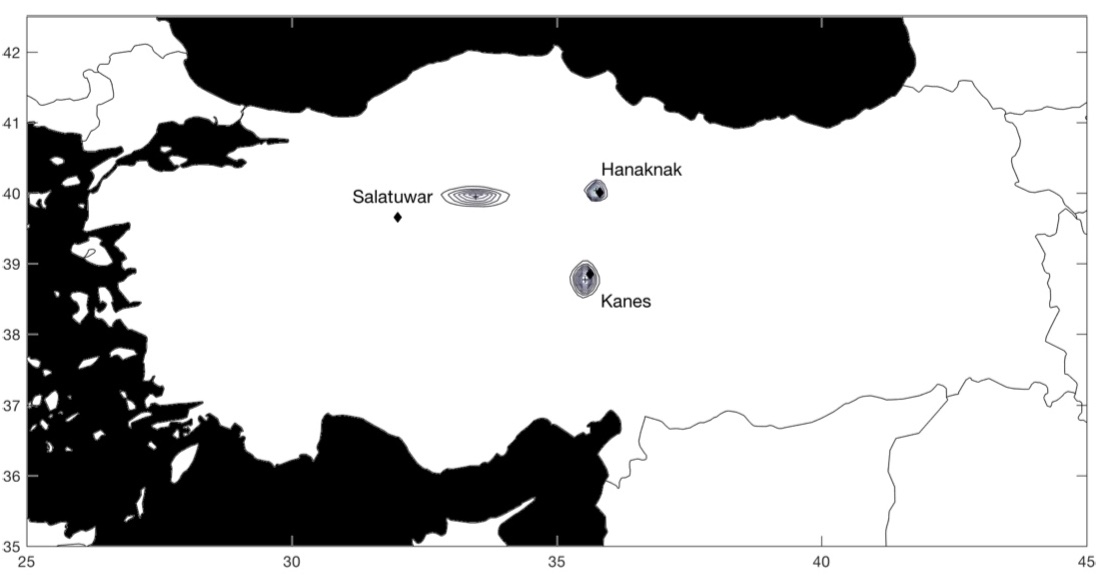
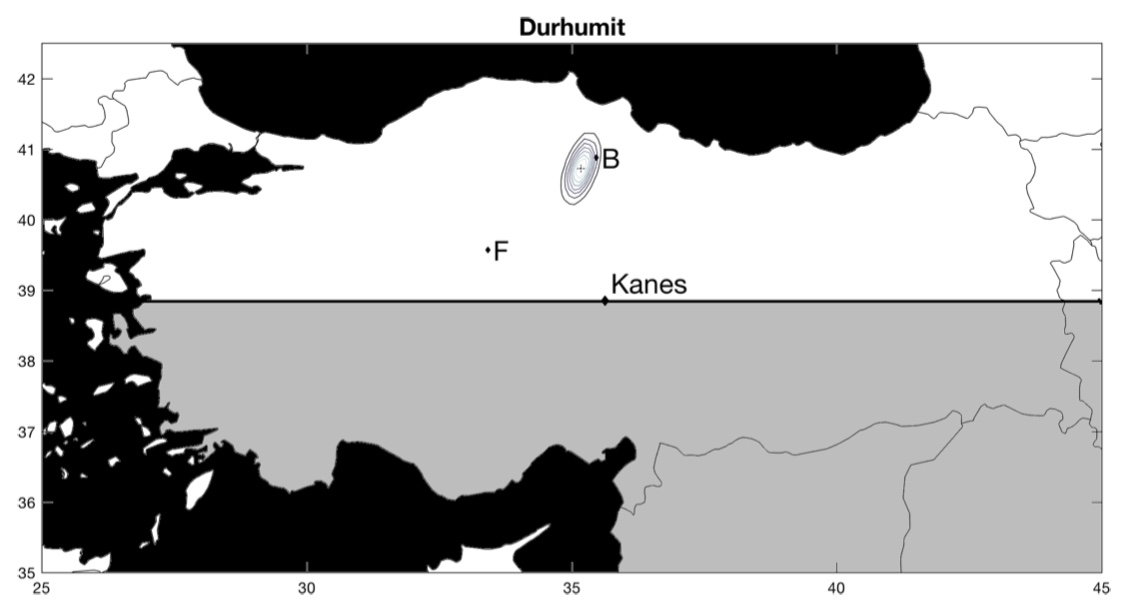
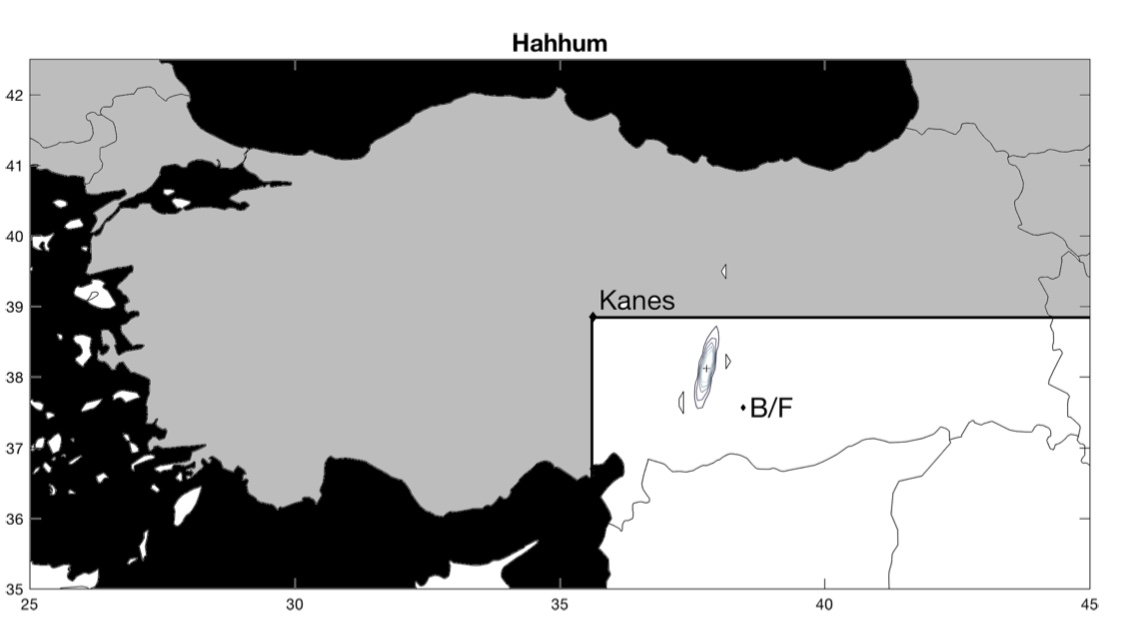
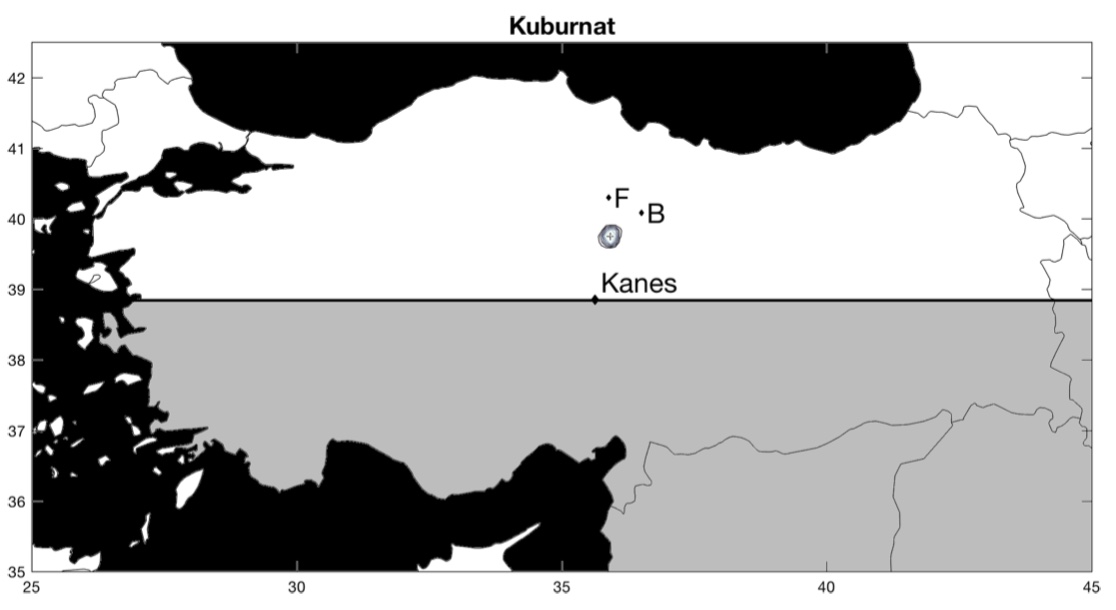
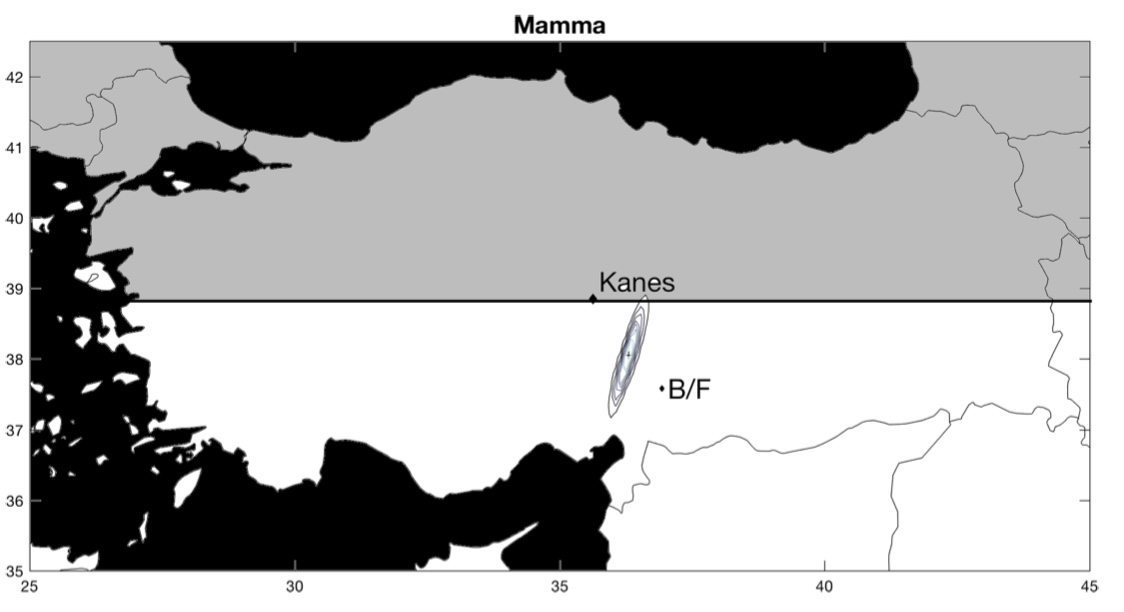
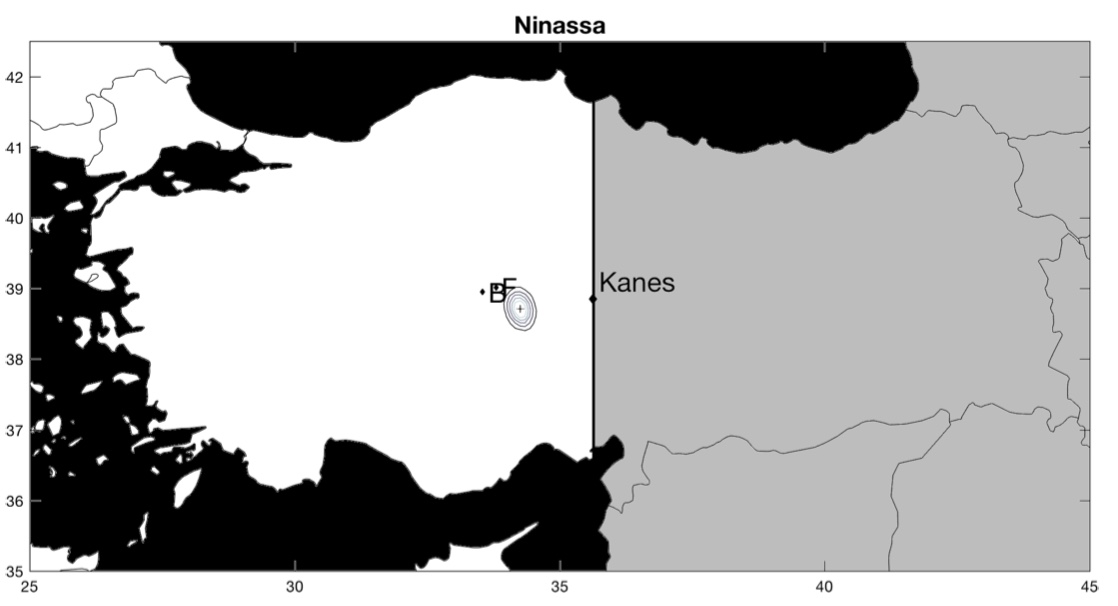
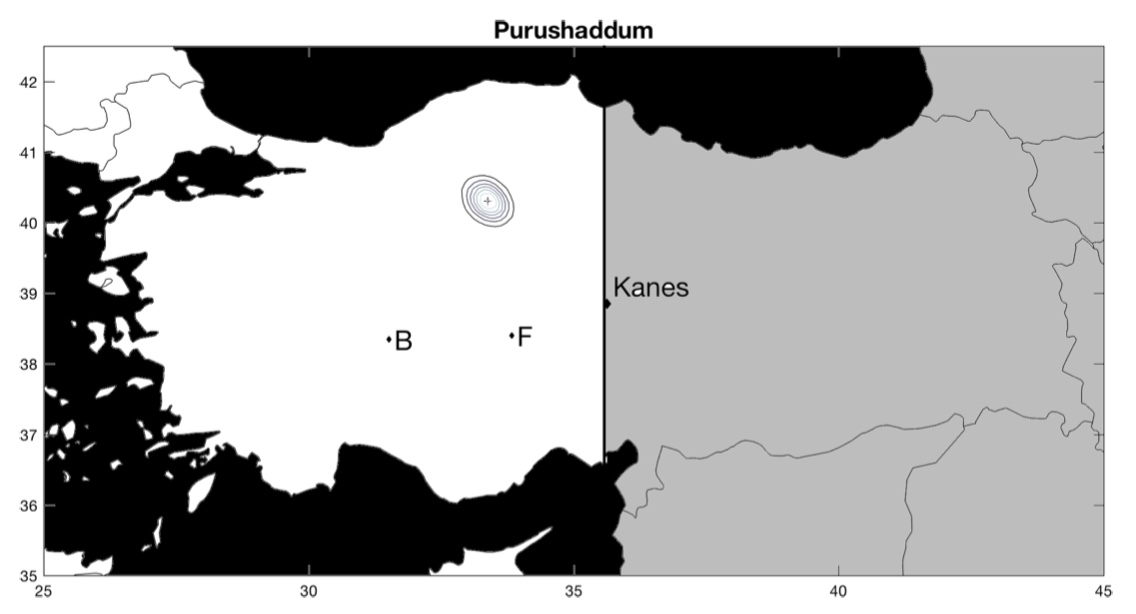
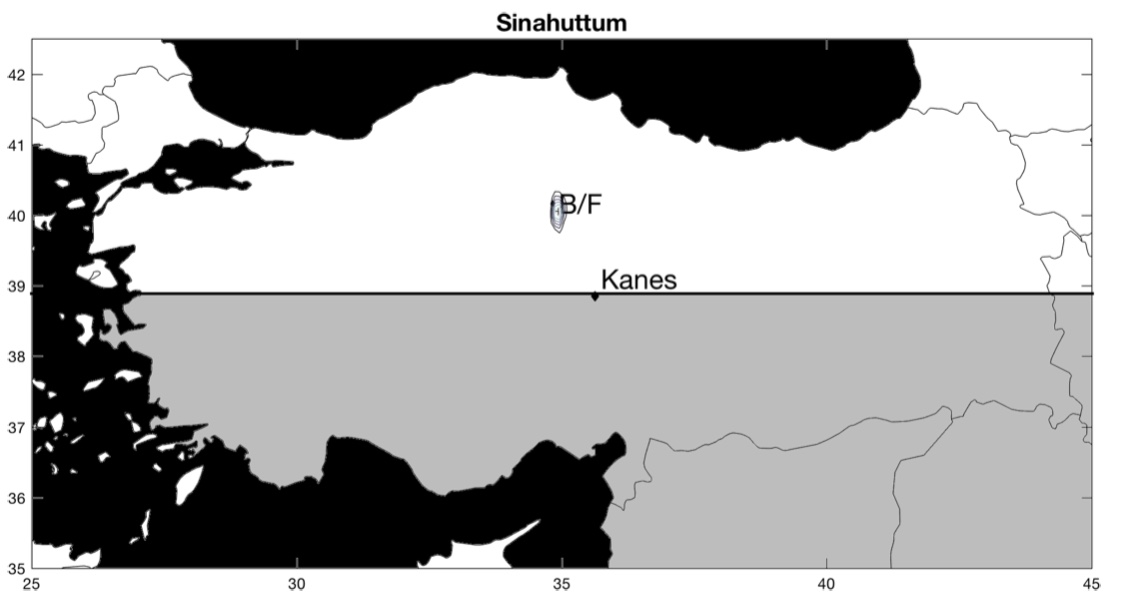
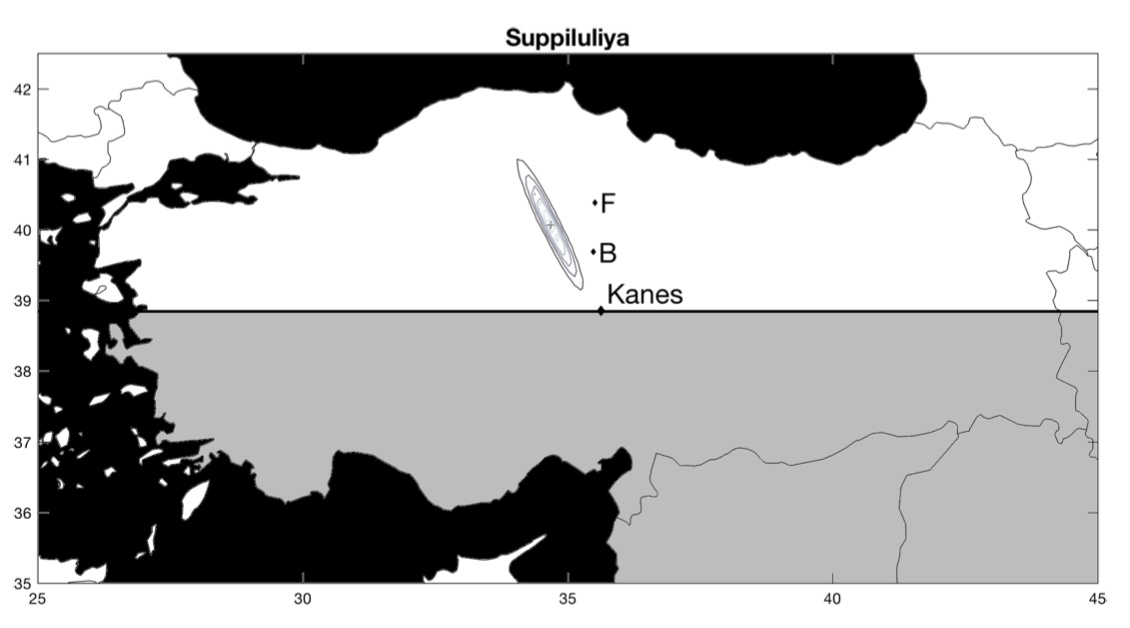
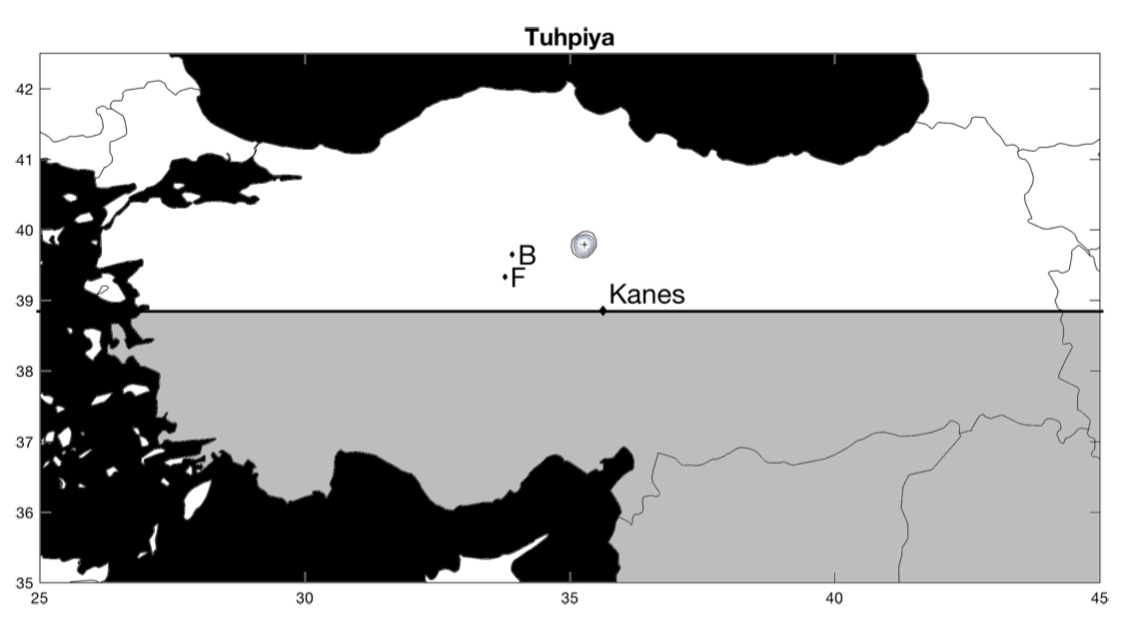
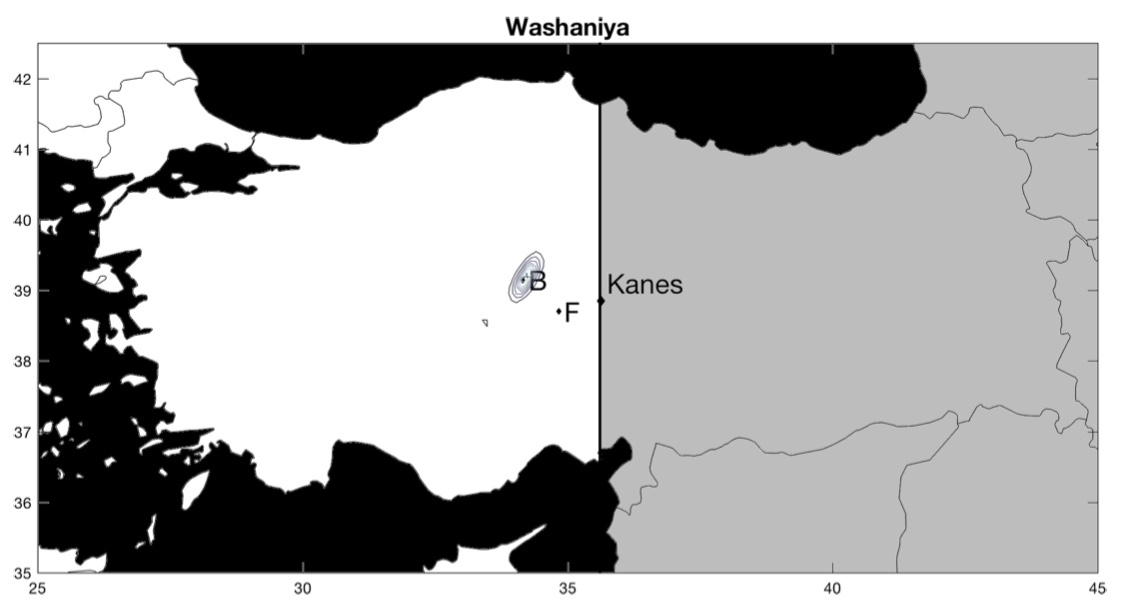
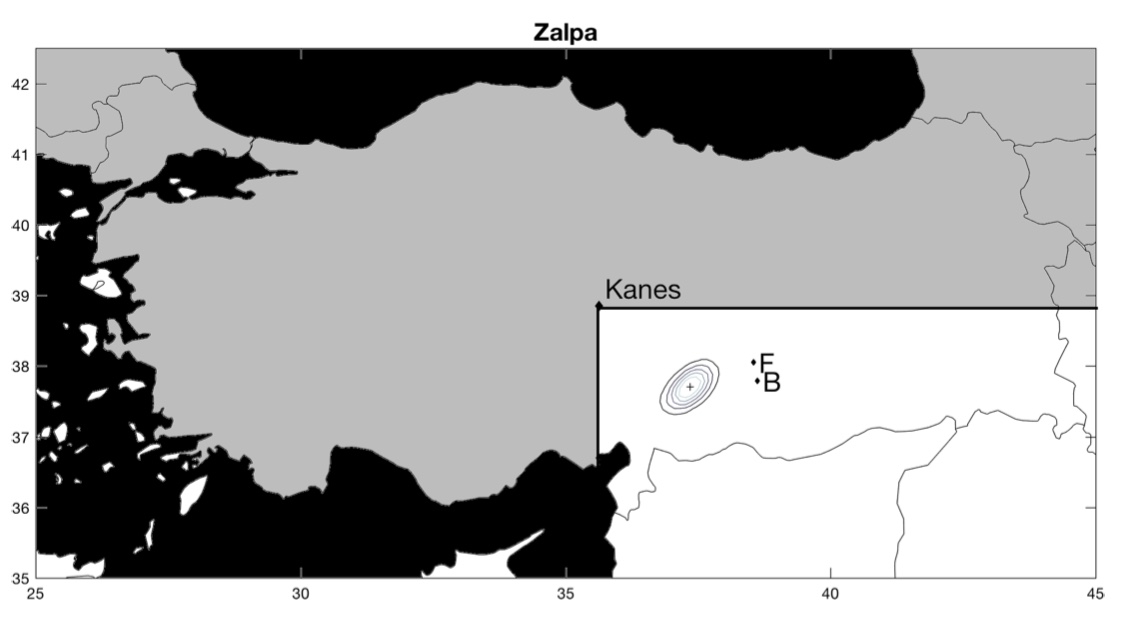
Maintenant, que se passe-t-il pour les cités dont la position est réellement inconnue ? Pour chacune de ces villes, les auteurs comparent leur estimation avec celle d’historiens (les lettres B et F¹« B » est pour l’estimation de l’historien Gojko Barjamovic et « F » pour l’estimation de l’historien Massimo Forlanini.). Parfois, leur estimation concorde, parfois, leur estimation ne concorde pas. Dans le premier cas, cela suggère que leur estimation valide celle de l’historien, dans le second cas, cela suggère que leur estimation invalide celle de l’historien. En cas de divergence, il est aussi possible que l’historien ait raison et que l’estimation des économistes soit fausse.

La ville de Kanes, dont la position est connue, sert de point de référence. La position estimée est représentée par une croix entourée de cercles concentriques. Les cercles représentent l’intervalle de confiance, c’est-à-dire le degré de précision de la position estimée : plus les cercles sont rapprochés les uns des autres, plus la position estimée est précise. Inversement, des cercles concentriques qui s’étendent sur une large zone suggèrent que la position estimée n’est pas très précise. En d’autres termes, plus les cercles concentriques couvrent une petite surface, mieux c’est !

Voici les résultats (pour zommer, cliquez sur les cartes) :

Plutôt impressionant ! Et je ne serais guère étonné que ce working paper soit publié dans une revue scientifique de très haut niveau.

Et vous, que pensez-vous de cette recherche ?

Image de converture : The Palaces at Nimrud Restored